

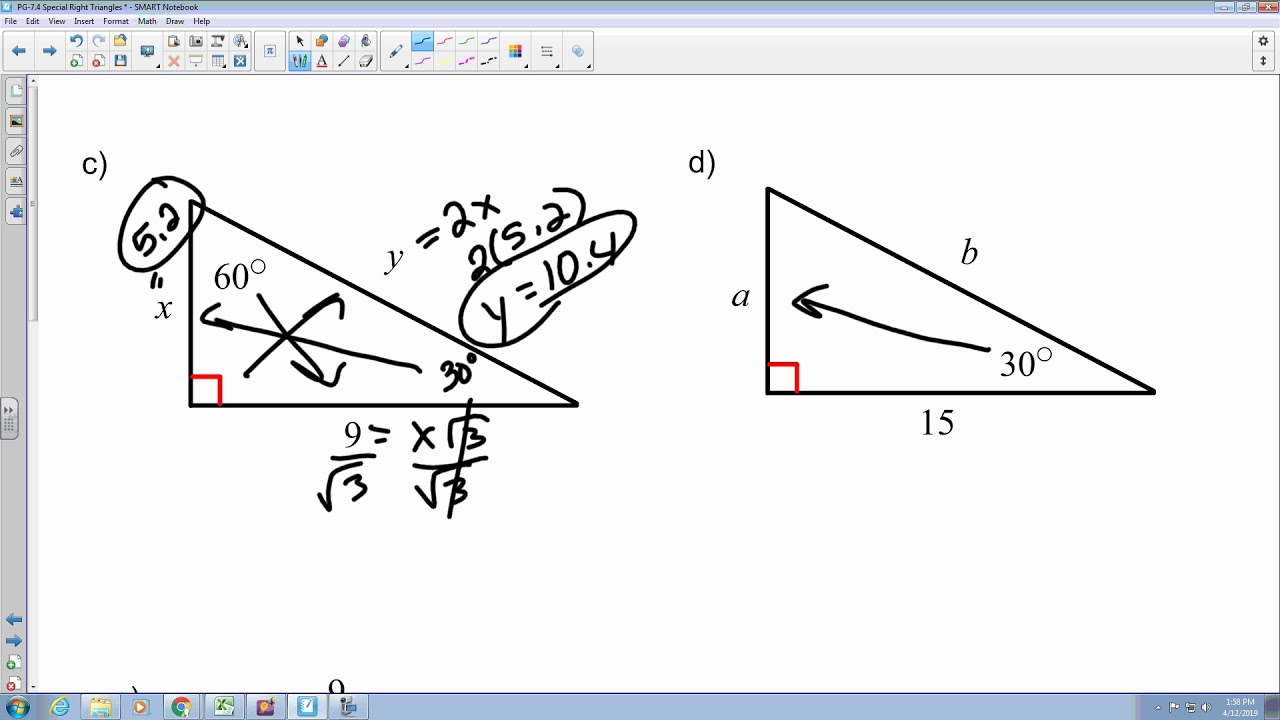
Highlighting the first letters of the functions and their ratios will be used to form a new mnemonic device. There are a couple of special types of right triangles, like the 45-45 right triangles and the. Look at the definitions of the new trigonometric funtions. A right triangle consists of two legs and a hypotenuse. It can be seen that the 's' from sine connects mathematically with 'c' from 'cosecant.' Similarly, the 'c' from 'cosine' goes together with the 's' from 'secant.'Īnother way to remember the new functions is to use a mnemonic device, like this one. Tangent and cotangent sound the same so, they are easily connected to each other.Īs for the other four, we can see that reciprocal functions can be remembered by looking at their first letters. Likewise, cosine and secant are reciprocal functions and tangent and cotangent are reciprocal functions, too. When we look at the definitions, we can see that sine and cosecant are closely related. Special Right Triangles Definition Special Right Triangles right triangles whose angle measures are 45 -45 -90 or 30 -60 -90. To remember these three functions, let's see how they relate to the first group of three functions. The Greek letter theta has been used to describe and them is typically used when describing the focus angle. The definitions of those functions can be found in the next graphic. This leaves us with the following triangle as it is viewed from angle 'A.'īesides the three main trigonometric functions, there are three other trigonometric functions: cosecant, secant, and cotangent. This is the side next to the angle in focus, as seen here. Last, we have the remaining side, called the adjacent side of the right triangle. So, the hypotenuse sits opposite angle 'C' in this diagram. The hypotenuse of a triangle is always the side furthest from the right angle. Look at this graphic to find the opposite side of the triangle.
We will focus on angle 'A' for the purposes of labeling the triangle's sides 'opposite,' 'adjacent,' and 'hypotenuse.' The opposite side of the triangle is the side furthest from the angle we are examining. So that we can see how they are used on triangles, let's look at a right triangle. This mnemonic device allows us to easily remember the definitions of these trigonometric functions. The 'S' with sine links together with 'O' and 'H' to form 'SOH.' Likewise, the letters 'CAH' go together as do 'TOA.' This leads us to a commonly used mnemonic device. To further abbreviate, look at the following highlighted portions of the definitions. The definitions would then look like this. Let's look at using 'O' for 'opposite, 'A' for adjacent, and "H" for hypotenuse. To help remember the definitions for the functions, many people abbreviate the definitions. These functions are used a considerable number of times in order to solve lengths of sides and measures of angles within right triangles. There are three main trigonometric functions: sine, cosine, and tangent.


 0 kommentar(er)
0 kommentar(er)
